SCIENCESDivision par zéroBackLien pour voir article source de WikipédiaUne division par zéro est, en mathématiques, une division dans laquelle le diviseur serait zéro. Ainsi, une division par zéro s'écrirait En algèbre, la division par zéro n'est pas définie. En analyse, sous certaines conditions, il est possible de calculer la limite d'un quotient dont le dénominateur est une suite ou une fonction de limite nulle. En informatique, une tentative de division par zéro cause une erreur qui peut, si le résultat n'en est pas testé, fausser le résultat du programme ou parfois en entraîner l'arrêt prématuré. Dans les machines fonctionnant avec le standard IEEE, le résultat en est simplement une configuration de bits particulière qu'on désigne sous le terme de NaN (
Explication de l'impossibilité de la division par 0L'explication qui suit est valable dans un anneau commutatif quelconque, c'est-à-dire un ensemble muni de deux lois (addition et multiplication) vérifiant les propriétés algébriques usuelles. En particulier, l'ensemble des nombres entiers (relatifs), celui des nombres réels, ou encore celui des nombres complexes rentrent dans ce cadre. On note 0 l'élément neutre de l'addition (le « zéro » en question), et 1 l'élément neutre de la multiplication. Il s'agit de montrer que zéro ne peut pas être un élément inversible de l'anneau. Si c'était le cas, en notant a l'inverse de zéro, on aurait, par définition d'un inverse, C'est pourquoi la division par zéro n'a non seulement pas de sens dans les ensembles de nombres usuels (entiers, réels ou complexes), mais plus généralement dans tout ensemble de nombres vérifiant les propriétés algébriques usuelles vis-à-vis de l'addition et de la multiplication (ce qu'on appelle un anneau). Il n'y a donc pas d'espoir de construire un nouvel ensemble de nombres qui donnerait un sens à l'inverse de zéro (comme celui des nombres complexes donne un sens à la racine carrée de − 1), sauf si l'on accepte de perdre des propriétés essentielles du calcul algébrique usuel (notamment la distributivité de la multiplication sur l'addition). Exemple de l'impossibilité de la division par 0Il s'agit d'une démonstration facile qui permet de prouver l'absurdité de la division par 0: si celle-ci est possible, il est en effet possible de montrer que 2 égal 1, ce qui écroule l'ensemble des mathématiques et conclut de la nécessaire impossibilité de la division par 0. Supposons a = b avec a et b réels. Notion de limite
Graphe de la fonction inverse
On ne peut ainsi pas donner de sens au quotient
et on dit que la valeur absolue de ce quotient admet pour limite « plus l'infini » lorsque x tend vers zéro. On écrit : et : |
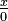 , où
, où  (ce qu'on pourrait noter aussi
(ce qu'on pourrait noter aussi  ). Mais, dans tout anneau, on montre aisément qu'on a, pour tout
). Mais, dans tout anneau, on montre aisément qu'on a, pour tout  (on dit que
(on dit que 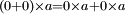 , et comme on a
, et comme on a 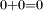 , cela entraîne, après avoir soustrait
, cela entraîne, après avoir soustrait 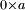 à chaque membre, l'égalité
à chaque membre, l'égalité 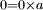 . On obtiendrait alors l'égalité
. On obtiendrait alors l'égalité  . Mais en
. Mais en  lorsque
lorsque  ,
, ) ou positives (le quotient tend alors vers
) ou positives (le quotient tend alors vers  ).
).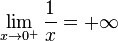 ,
, .
.